ハノイの塔 (tower of Hanoi) について考えてみようと思います。 ハノイの塔は数学パズルみたいな物です。 プログラミングの練習問題としてよく使われます。
目次
コンソール上で動く「ハノイの塔」のプログラム
コンソール上で動くハノイの塔のプログラムを作りました。 今回、棒の並びは移動元A(from), 予備B(spare), 移動先C(to) とします。
特に真新しい事はしていません。 行を上書きする形で、移動の様子を出力しただけです。 上書き出力すると、アニメーションぽくなります。
出来栄えはともかく、とりあえず、動きます。 Pythonがインストールされてるなら、ダブルクリックするだけで動きます。 必要ならソースコードのパラメータを変更してください。
「ハノイの塔」のルール
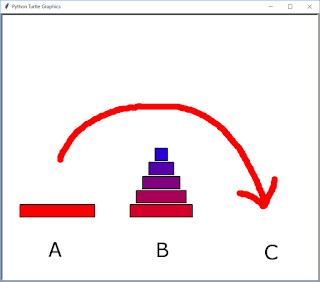
n枚の円盤の塔を棒Aから棒Cに移動させます。ただし、以下のような制限があります。
- 円盤(disk)の大きさは全て異なる
- 棒(rod)はA, B, Cの計3本ある
- 棒Aは移動元, 棒Bは予備, 棒Cは移動先とする
- 一番上の円盤は他の棒に移動できる
- 円盤の塔は常にピラミッド状である(大きな円盤の上に小さな円盤がある)
上の図では、棒が省略されてますけど、 下のような画像をイメージしてください。
「ハノイの塔」のアルゴリズム
図で説明
円盤の塔が振り子のように 棒A と 棒B を複雑に往復しながら、 1個ずつ一番下の円盤(disk)を 一番右の棒C に投げる感じです。 ※もちろん、棒Cも作業場所として使います。
まず、Aにある一番下以外の円盤(n-1)枚 を何回も複雑に移動させて、 Bに (n-1)枚の円盤の塔 を作ります。 この図の場合、(n-1) = (6-1) = 5 枚。
すると、Aの一番下にある円盤1枚はCに移動できます。
この結果、いま、A が空きました。 Bに 5枚の円盤の塔 があります。
だから、Bの一番下以外の円盤4枚 を複雑に移動させて、 Aに 4枚の円盤の塔 を作る事ができます。
すると、Bの一番下の円盤1枚 は Cに移動できます。
この結果、B が空きました。Aには4枚の円盤の塔があります。 だから、Aにある一番下以外の3枚の円盤 をBに移動させます。
すると、Aにある一番下の円盤1枚 はCに移動させることができます。
説明するのが面倒になってきたので、この先は読者の想像に任せます。
ここまでの作業を簡潔にたった一言で言い表します。
「塔の一番下の円盤を移動させるには、その上にある円盤を全部どかさないといけない」
「ハノイの塔」のアルゴリズムのまとめ
move(n, from, to, spare) : n枚の円盤を from から to に移す関数
と定義します。 spare も作業場所として使えます。
棒A から 棒C に n枚の円盤を移す事、つまり、move(n, A, C, B) を考えます。
- 一番下以外の(n-1)枚の円盤を A から B に移す(何回も円盤を動かして、上にある円盤を移動させる)
- これは move(n-1, A, B, C) と同じこと
- すると、一番下の円盤1枚を A から C に移すことができる(1回で動かせる)
- これは move(1, A, C, B) と同じこと
- その結果、A が空になり、B に(n-1)枚の円盤の塔ができる
- A を予備、 B を移動元 とみなせる。※移動先は常にCのまま
- n は(n-1)になっている
- B から C に (n-1)枚 の円盤を移す( 残りの (n-1)枚 を処理 )
- これは move(n-1, B, C, A) と同じこと
実際に、どうやって円盤を移動させるか考えると、結構複雑なので混乱するかもしれません。 でも、再帰的にmove関数を定義したら、 ハノイの塔の問題は、不思議なくらいシンプルなプログラムとして表すことができます。
再帰的なアルゴリズムを数学でたとえます
ハノイの塔のアルゴリズムは 再帰的(recursive) です。 再帰的の意味を数学を使って説明します。
nの階乗(n!)の再帰的なアルゴリズム
nの階乗(n!) を例として、再帰的アルゴリズムの感覚を説明します。
f(n) = n * f(n-1) , f(0) = 1 のとき、f(4) の値を求めるとします。 (*は掛け算の記号です)
f(4)は以下のように展開できます。
f(4)
= 4 * f(3)
= 4 * (3 * f(2))
= 4 * (3 * (2 * f(1)))
= 4 * (3 * (2 * (1 * f(0))))
上のように展開したら、一番内側の 1 * f(0) = 1 * 1 = 1 を求めて、 外に巻き戻っていく感じで掛け算します。
= 4 * (3 * (2 * (1 * f(0) ) ) )
= 4 * (3 * (2 * (1 * 1) ) )
= 4 * (3 * (2 * 1 ) )
= 4 * (3 * 2)
= 4 * 6
= 24
「再帰的」と「繰り返し」の違い
forループやwhileループを使い、nの階乗(n!) を求めることもできます。 そのアルゴリズムは繰り返し的(iterative) です。
4 = 4
4*3 = 12
4*3*2 = 24
4*3*2*1 = 24
上のように、「順番に数を掛けるのを繰り返す」 みたいなアルゴリズムが繰り返し(iteration)のアルゴリズムです。
一方、再帰的に関数を展開して、一番中の値を求めて、 外に巻き戻って計算する、みたいなアルゴリズムが再帰的なアルゴリズムです。 両者は似てるようで違います。
繰り返し的なアルゴリズムが計算効率の面では勝ってると思います。 でも、再帰的なアルゴリズムのほうが芸術的な気がします。
フィボナッチ数列は再帰的な数列だし、フラクタル図形は再帰的な図形です。 再帰的アルゴリズムは自然界のアルゴリズムといえるのではないでしょうか。
グラフィカルな「ハノイの塔」のアニメーション
タートルグラフィックス (Turtle Graphics) というグラフィックライブラリを使えば、 ハノイの塔をグラフィカルなアニメーションで表す事ができるらしいです。 タートルグラフィックスのデモスクリプトに「ハノイの塔」があったので紹介します。
タートルグラフィックス(turtleモジュール) は プログラミング言語Python に標準装備されているライブラリです。 Pythonをインストールしているのであれば、 コマンドプロンプトで下のコマンドを入力すれば、 「ハノイの塔」のアニメーションが始まります。
python -m turtledemo.minimal_hanoi
デモスクリプト実行用のヴューアーを使いたい場合は 下のコマンドを入力してください。ソースコードを見ることもできます。
python -m turtledemo
いろいろなデモスクリプトがあります。
Turtle Graphicsを使えば、プログラミングでお絵かきできるので、 遊んでみると楽しいです。 タートルグラフィックスのようなライブラリ使えばいろんな言語でお絵かきできます。







0 件のコメント:
コメントを投稿
投稿されたコメントは承認後に公開されます。