【Python】中国の国旗を描きました【タートルグラフィックス】

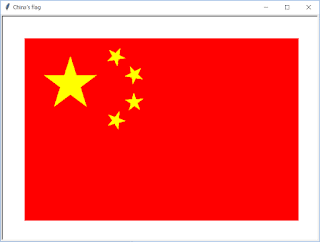
前回の記事で描いた日本国旗に続き、今回、中国国旗を描きました。タートルグラフィックスを使って。

中国国旗を描くのは簡単そうに見えて少しむずかしいです。小さい星★が回転してるので。星型図形についての幾何学的な分析が必要でした。絵を描いているというより数学の問題を解いてる感じでした。

中国国旗を描くプログラムのソースコード
数学的な分析
中国の国旗は意外に細かい

中国国旗を描くプログラムのソースコード

中国国旗を描くプログラムのソースコードはこちら。draw_china_flag_margin1inch_20180510.py というファイルです。 Pythonをインストールしている人はpythonファイルをダブルクリックするだけで、このプログラムを動かすことができます。

上のgifアニメーションのように、上下左右に1インチの余白を入れました。余白を入れなかったら、端を描いてる様子が見えなくなるからです。

import turtle
import math

def deg2rad(degrees):
    return degrees * (math.pi/180)

def rad2deg(rad):
    return rad * (180/math.pi)

THETA = deg2rad(18.0)
SIN18 = math.sin(THETA)
COS54 = math.cos(3*THETA)
LENGTH0 = 4 * SIN18 * COS54

#----------星を描く関数----------
def drawstar(ttl, centerX, centerY, radius, angle):
    #----------長さや角度の設定----------
    n = 5
    in_angle = 180/n # 内角(星の尖ってる角度)
    ex_angle = 180 - in_angle # 外角
    length = radius * LENGTH0 # 星の輪郭の一辺の長さ
    #----------移動----------
    rad = deg2rad(angle)
    x = centerX + radius * math.cos(rad)
    y = centerY + radius * math.sin(rad)
    ttl.penup()
    ttl.goto(x, y) # 最初の点の移動
    #----------最初の線を引く方向を向く----------
    initial_heading = angle+162 # 最初の線を引く方向
    ttl.setheading(initial_heading) #最初の線を引く方向を向く
    ttl.pendown()
    #----------星を描く----------
    ttl.begin_fill()
    for i in range(n):
            ttl.fd(length)
            ttl.rt(ex_angle/2)
            ttl.fd(length)
            ttl.lt(ex_angle)
    ttl.end_fill()

#---------長方形を描く関数---------
def draw_rectangle(ttl, x, y, width, height):
    ttl.penup()
    ttl.goto(x, y)
    ttl.setheading(0)
    ttl.pendown()
    for i in range(4):
        if i % 2 == 0:
            ttl.fd(width)
            ttl.rt(90)
        else:
            ttl.fd(height)
            ttl.rt(90)


# 旗のサイズ ( width : height = 3 : 2)
width = 3 * 200
height = 2 * 200

# 中国国旗の詳細情報より
ux = width / (2.0*15)
uy = height / (2.0*10)

# 絵を描く画面を設定する
wn = turtle.Screen()
wn.title ('China\'s flag')
wn.setup (width+100, height+100, 0, 0)

# カーソルを設定
ttl = turtle.Turtle()
ttl.speed(5)
ttl.screen.screensize(width+100, height+100)

#----------------赤い長方形を描く----------------
ttl.pencolor('red') # ペンを赤色に設定
ttl.fillcolor('red') # 塗りつぶしの色を赤色に設定
ttl.begin_fill()
draw_rectangle(ttl, -width/2, height/2, width, height)
ttl.end_fill()

#---------------- 星を描く ----------------
ttl.pencolor('yellow') # ペンの色を黄色に設定
ttl.fillcolor('yellow') # 塗りつぶしの色を黄色に設定

# 大きな星を描く
x = -width/2 + 5*ux
y = height/2 - 5*uy
drawstar(ttl, x, y, 3*ux, 90 )

# 上から1番目の小さな星を描く
x = -width/2 + 10*ux
y = height/2 - 2*uy
angle = 180 + rad2deg(math.atan(0.5))
drawstar(ttl, x, y, ux, angle)

# 上から2番目の小さな星を描く
x = -width/2 + 12*ux
y =  height/2 - 4*uy
angle = 180 + rad2deg(math.atan(1.0/7.0))
drawstar(ttl, x, y, ux, angle)

# 上から3番目の小さな星を描く
x = -width/2 + 12*ux
y =  height/2 - 7*uy
angle = 180 - rad2deg(math.atan(2.0/7.0))
drawstar(ttl, x, y, ux, angle)

# 上から4番目の小さな星を描く
x = -width/2 + 10*ux
y = height/2 - 9*uy
angle = 180 - rad2deg(math.atan(4.0/5.0))
drawstar(ttl, x, y, ux , angle)

ttl.hideturtle() # カーソルを隠す
wn.exitonclick() # クリックしたら終了

数学的な分析

星型図形の特徴

この星型図形は五芒星（ごぼうせい）と呼ばれているらしいです。英語でいうと、pentagram　です。

一筆書きできます。

星型図形を描く手順

以下が（複合型以外の）星型図形を一筆書きで描くアルゴリズム（手順）です。反時計回りに線を引くことにします。

星型図形の頂点を向く
星型図形の頂点に飛ぶ
162°左を向く（最初の進行方向）
*** 繰り返しの処理（5本の線を引く）***
1. そのまま直進して線を描く
2. 線の端まで来たら144°左に向きを変える

星型図形を描くプログラムのソースコードはこちらです。ファイルをダブルクリックしたらプログラムが動きます。

星型図形を塗りつぶすとしたら、一筆書きしたあと塗りつぶす方法、外側の輪郭を描いたあと塗りつぶす方法の二通りがあると思います。

~~一筆書きしたあと塗りつぶす方法（左上）は難易度がすこし高いです。三角関数を利用した幾何学的な計算がかなり必要だからです。~~

計算があってるかあまり自信なかったけど、外接円をキレイに描けてるので、正しかったみたいです。

半径1の円に内接する星型図形を考える

半径R0(=1)の円に内接する星型図形を考えます。円が外、星型図形が中です。辺の長さを下のように定義します。

P0: 外側の五角形(Pentagon)の辺の長さ
P1: 内側の五角形(Pentagon)の辺の長さ
S0: 星型図形(Star polygon)の辺の長さ
R0: 五角形に外接する円の半径(Radius)
D0: 五角形の対角線(Diagonal) の長さ

$\begin{eqnarray} P_0 & = & 2 \cos 54^\circ = 2 \sin 36^\circ (\fallingdotseq 1.1755705045849463) \\ P_1 & = & P_0 R_1 = 2 \frac{\cos 54^\circ \sin 18^\circ} { \cos 36^\circ}(\fallingdotseq 0.4490279765795853) \\ P_n & = & P_0 R_1^{n} \\ S_0 & = & \frac{\cos 54^\circ} {\cos 36^\circ}(\fallingdotseq 0.7265425280053609)\\ R_0 & = & 1 \\ R_1 & = & \frac{\sin 18^\circ} {\cos 36^\circ}(\fallingdotseq 0.3819660112501051) \\ D_0 & = & 2 \cos 18^\circ (\fallingdotseq 1.902113032590307)\\ & = & 2 S_0 + P_1 = 2 \frac {\cos 54^\circ}{ \cos 36^\circ} + 2 \frac{\cos 54^\circ \sin 18^\circ} { \cos 36^\circ} \\ \end{eqnarray}$

20180511-pentagram.tex

この星型図形は回転対称（Rotational symmetry）の図形です。 72度回転したら元の図形と一致します。だから、外接円の半径は星型図形の大きさを表す指標として適しているでしょう。

半径の長さが1の円を考える理由

なぜ半径の長さが1の円を考えるのか。そんな不思議なことではありません。私たちがふだん使っている単位（例えば、秒速や時速）と本質的に同じことです。

「秒速 9mの速さ」　と「9.9秒で89.1m進む速さ」のどちらが想像しやすいでしょうか。 1秒という長さが一番身近だから秒速のほうが想像しやすいです。また、秒速で速度が与えられたら、進んだ距離の計算がしやすいです。 5秒で何m進むか計算してみます。

秒速9mの速さ：
9[m/s] * 5 [s] = 45[m]
9.9秒で89.1m進む速さ：
(89.1[m] / 9.9[s]) * 5[s] = 45[m]

秒速で速度が与えられたら、秒速に秒を掛けるだけで、進んだ距離が計算できます。

半径1を考えるのも同様です。1を基準にして計算しやすくするためです。ちなみに半径1の円は単位円(unit circle)と呼ばれています。

もし、「半径10の円に接する星型図形の辺の長さ」を計算したければ、「半径1の円に接する星型図形の辺の長さ」を10倍すればいいです。

「一定の長さの線を引き、一定の角度向きを変える」のを繰り返すと、一番最初の場所に戻ってくる

引いた線のベクトルの和が0になるからです。別のページで詳しく説明します。

「円周を144°進んだら点を打つ」のを繰り返すと、円周が5等分される

「144*1, 144*2, 144*3, 144*4, 144*5 を360で割った余り」が全て異なり、かつ、全ての余りは72の倍数で表されるからです。別のページで詳しく説明します。

中国の国旗は意外に細かい

中国国旗の左上にある星は適当に並んでると思っていましたが、小さな星の頂点は大きな星の中心を指しています。だから、星型図形を回転させて描く必要がありましいた。

星が回転する角度を求めるのにtan(タンジェント)の逆関数である arctan (アークタンジェント）を使いました。アークタンジェントは mathモジュールのなかでmath.atan(x) と定義されています。だから、math.atan(x)を使うために、プログラムの最初の部分で import math と記述します。

mathモジュールの三角関数が扱う角度の単位はラジアン(radian)です。度ではありません。でも、turtleモジュール (タートルグラフィックスを使うために取り込むプログラムの部品みたいな物）では、度が角度の単位として使われているので、混乱しないようにしましょう。 ※radians()という関数を使えば、角度の単位がラジアンになるらしいです。

上の図のように、すべての星の正確な座標が決められてるらしいです。詳細はFlag_of_China(ウィキペディア英語版) にかいてありました。

次はアメリカ国旗を描きます。

特訓中