【幾何学】一筆書きで星型正多角形を描く【代数学】

今まで、プログラミング言語Pythonとタートルグラフィックスを使って星型図形を描きました。一筆書きで星型多角形を描いていて、面白そうな発見があったので、それを簡単に証明しようと思います。

「一定の角度向きを変え、一定の長さの線を引く」のを繰り返すと、一番最初の場所に戻ってくる
1. 十二芒星を例に説明
2. カーソルが最初の場所に戻ってくることを証明
「円周をθ°進んだら点を打つ」のを繰り返すと、円周がgcd(360,θ)°刻みで均等に分割される

「一定の角度向きを変え、一定の長さの線を引く」のを繰り返すと、一番最初の場所に戻ってくる

十二芒星を例に説明

12芒星を作るために、12本の線を引きましたが、その12個のベクトルの和を計算すれば、0ベクトルになります。つまり、最初の頂点に戻ってきます。

もし、線を中心に集めたとしたら下のgifアニメーションのようになります。

つまり、「カーソルが一番最初あった所に戻ってくる現象」を分かりやすく説明するならば、「"円周をn等分したn個の点”の重心」が「円の中心」である事と同じ意味です。下の図でいうと、「12個の青い点の重心」は「円の中心」です。

それを証明するのには三角関数の計算が必要です。

カーソルが最初の場所に戻ってくることを証明

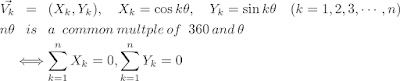
$\begin{eqnarray*} \vec{V_k} & = & (X_k, Y_k) ,\hspace{10} X_k= \cos{k\theta}, \hspace{10} Y_k= \sin{k \theta} \hspace{10}(k=1, 2, 3, \cdots, n) \\ n\theta & is & a\hspace{5} common\hspace{2} multple\hspace{2} of\hspace{5} 360\hspace{2} and \hspace{2}\theta \\ & \Longleftrightarrow & \sum_{k=1}^n X_k = 0, \sum_{k=1}^n Y_k = 0 \end{eqnarray*}$

一番最初, カーソルは右（0度）を向いているとする。「左（反時計回り）にθ度向きを変えて、1の長さの距離を進む」のを繰り返すことにすると、ある本数（n本とする）の線を引いたとき、カーソルは一番最初に点に戻ってくる。

なぜなら、k本目の線をベクトルVk=(Xk Yk)とみなすと、 Xk = cos kθ, Yk = sin kθ (k=1,2,3,..., n)と表すことでき、「nθ が “360とθの公倍数” である」ときに限り、「ΣXk = 0 かつ ΣYk=0」が成り立つからである。

上の式を証明するのに、いわゆる「三角関数の積和の公式」を使っています。

たぶん計算結果は正しいと思います。

(cos A, sin A) = (cos B, sin B) が成り立つとき、 AとBは同じ方向の角度です。 360度の倍数の角度差があるかもしれませんが、向きは同じ。

少し論理的に整理すると、
(cos A, sin A) = (cos B, sin B) ⇔ 「“cosA = cosB” かつ “sinA = sinB”」

したがって、上の計算過程の２式（上から6番目）より、

「ΣXk = 0 かつ ΣYk=0」
⇔ 「“sin θ/2 = sin(nθ + θ/2)” かつ “cos θ/2 = cos(nθ + θ/2)”」
⇔ nθ は 360の倍数 (∵ nθ＞0)
⇔ nθ は “θと360の公倍数”（∵ nθはθの倍数でもある）

つまり、「nθ が “360とθの公倍数”」⇔「ΣXk = 0 かつ ΣYk=0」が言えます。

「円周をθ°進んだら点を打つ」のを繰り返すと、円周がgcd(360,θ)°刻みで均等に分割される

十二芒星を考えてみる

例えば、上のgifアニメーションのように、「円周をθ=150°進んで点を打つ」のを最初の点に戻るまで繰り返すと、円周が gcd(360,150)=30° 刻みで均等に12分割されます。 gcd(360,150)は360と150の最大公約数のことです。

ついでに、点と点を線でつないだら、十二芒星（dodecagram)ができます。頂点は「アナログ時計の数字」と同じような位置に配置されています。下の図の円周にある数字は「回転した角度」です。

通常、右を0度として、反時計回りに角度を測ります。右が0度、上が90度、左が180度、下が270度、1周して右が360度の向きです。しかし、カーソルが円周を何回転もしてるので、「360度以上になってる角度」がたくさんあります。

証明すること

「“円に内接する星型正n角形”のn個の頂点」は円周をn等分しています(上の図で言うと、n=12, θ=150)。つまり、以下のことが言えます。

「θ,2θ,3θ, ..., nθ を360で割った余り」がすべて異なる（nは頂点の個数。nθが「360とθの最小公倍数」の時、最初の点に戻ってくる事は上で証明済み）
全ての余りは「360とθの最大公約数」の倍数で表すことができる
n=360/gcd(360,θ)である

「360度以上になっている角度」を０以上～360未満で表すには、360で割った余りを計算します。 360を360で割った余りは0。450を360で割った余りは90。

「人生が360度変わった」＝「人生の向きが全く変わってない」。
「人生が450度変わった」＝「人生が90度だけ変わった」。

「θ,2θ,3θ, ..., nθ を360で割った余り」の計算法もそれと全く同じです。「kθが何回転した角度であるか」はどうでもよくて、kθがどの方向を向いているかを知りたいので、 kθを360で割った余りを計算します。上の図のように。

450≡90 は「450,90を360で割った余りが等しい」という意味。もう少しちゃんと書くなら、 450≡90 (mod 360)です。

最小公倍数と最大公約数

「360とθの最小公倍数（least common multiple)」は lcm(360,θ) と表記する事ができます。「360とθの最大公約数（greatest common divisor)」は gcd(360,θ) と表記することができます。

「aとbの最大公約数」とは、自然数a,bを掛け算で表したとき、共通する掛ける数字の部分です。例えば、56と140の最大公約数は、「56=2*2*2*7」「140=2*2*5*7」より gcd(56,140)=2*2*7=28。

「aとbの最小公倍数」とは、「“aの倍数であり” かつ “bの倍数である” 数」のうち、一番小さい数です。「 “aにないbの約数” をaに掛ける」または「“bにないaの約数” をbに掛ける」と求めることができます。つまり、「lcm(a,b) = (a*b)/gcd(a,b)」 です。

例えば、56と140の最小公倍数は280です。 a*b も「aとbの公倍数」ですが、aとbに共通の約数がある時、最小公倍数はもう少し小さくなります。

「kθ,lθを360で割った余り」は異なる

「kθ, lθ を360で割った余り」が同じ場合、「kθとlθの差」が 360の倍数になります(ただし、1≦k＜l≦n かつ k≠l　とする)。今回の場合、余りがすべて異なることを示したいので、「kθとlθの差」が360の倍数にならない事を示します。

「 1 ≦ l-k ＜ n 」より、(l-k)θ は 360の倍数にはなりません。「360とθの最小公倍数」が nθ なので、「θにn倍未満の正の整数を掛けた (l-k)θ」は 360の倍数にはなりません。最小公倍数より小さい公倍数はありませんから。

したがって、n個の余りは全て異なる値です。

全ての余りは「360とθの最大公約数」の倍数で表すことができる

pθを360で割った余りは, 「pθ - 360q」と表すことができます。 qは商です。

d = gcd(θ, 360) とします。すると、

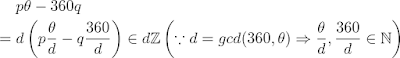
$\begin{eqnarray} & & p\theta - 360q \nonumber \\ & = & d \left(p {\theta \over d} - q {360\over d} \right) \in d \mathbb{Z} \left(\because d=gcd(360,\theta) \Rightarrow {\theta \over d} ,{360\over d} \in \mathbb{N} \right) \nonumber \end{eqnarray}$

となるので、「pθを360で割った余り」はdの倍数になります。 dの倍数どうしで足し算や引き算をしたら、その演算結果はdの倍数のままという事です。

数学用語でいえば、dの倍数(0や負の整数も含む)は加減の演算に関して閉じている(closed)と言えます。こういう話に興味がある人は群論(group theory)の本をよんでください。

nθ =「360とθの最小公倍数」のとき、初めて一番最初の点に戻ってくるので、

$\begin{eqnarray} n \theta & = & lcm (360,\theta) \\ n & = & {lcm(360,\theta) \over \theta} \\ & = & {360 \theta \over gcd(360,\theta)} {1 \over \theta} \\ & = & {360 \over gcd(360,\theta)} \end{eqnarray}$

つまり、360度の円周を「360とθの最大公約数」度ごとに分割するには、n個の異なる点が必要です。

結論

「θ,2θ,3θ, ..., nθ を360で割ったn個の余り」は「gcd(360,θ)の倍数」で表され、「gcd(360,θ)の倍数の角度」は円周上に n=360/gcd(360,θ) 個だけある。 n個の余りが全て異なるので、同じ角度の点は無く、きれいに散らばっていて、円周をn等分している。

特訓中