2018年6月2日土曜日

【Python】ハート型の図形を描きました【タートルグラフィックス】【matplotlib】

turtleモジュール や matplotlibライブラリ を使用して、ハート型の図形を描きました。 使用したプログラミング言語はPythonです。

直線と弧を組み合わせて描いたハート(turtleモジュール使用)

図形的特徴

曲線の部分は円です。ほかの線は直線です。 作図して、角度や長さを計算しました。 そして、作図したデータをもとに、turtleモジュールを使い、お絵かきしました。

最適な角度を調整した結果、「扇形の中心角θ」 は 210°、「直線と水平軸の角度α」 は 45°になりました。シンプルにθ=180°としても良かったかもしれません。

ハートを描くプログラム(turtleモジュール使用)のソースコード

これが ハート型の図形を描くプログラムのソースコード です。 

# tutleモジュールをインポートします。タートルグラフィックスのことです。
import turtle

# mathライブラリから、関数cos(),sin() と 円周率piをインポートします
from math import cos,sin, pi

# 円周率は定数なので、なんとなく大文字PIで表記しました。別に小文字のままpiで問題ないと思います
PI=pi

# ハートを描く関数です。
def draw_my_heart(ttl, x, y, radius, alpha=45, theta=210, degrees=0):
    ttl.setheading(degrees) # カーソルの向きを設定する。右0度,上90度,左180度,下270度。
    ttl.penup() # ペンを上げる（ペンを上げると、移動中に線が引かれない）
    ttl.goto(x, y) # カーソルが(x,y) の座標に移動する
    ttl.pendown() # ペンを下ろす（ペンを下ろすと、移動中に線が引かれる）

    # 長ったらしい数式を書くので、変数を短めにしました
    r = radius # 扇形の半径
    a = alpha # 水平方向と直線の角度
    t = theta # 扇形の中心角

    # 直線の長さです。作図して求めました
    straight = r*(-cos((a+90)*PI/180)-cos((t+a-90)*PI/180)) / cos(a*PI/180)

    ttl.left(a) # 左にa度カーソルの向きを変えます
    ttl.forward(straight) # カーソルが向いてる方向にstraightの長さ進みます。右の直線部分。
    ttl.circle(r,t) # 半径rでt度の扇形を描きます。右側の扇形。
    ttl.left(720-2*a-2*t) # 真ん中で左に(720-2*a-2*t)度カーソルの向きを変えます。作図して求めた角度。
    ttl.circle(r,t) # 半径rでt度の扇形を描きます。左側の扇形。
    ttl.forward(straight) #カーソルが向いてる方向にstraightの長さ進みます。左の直線部分。

width=700 # 画面の横幅
height=700 # 画面の高さ
x = 0 # ハートの一番下の点のx座標
y = -150 # ハートの一番下の点のy座標
r = 100 # ハートの扇形の半径

scr = turtle.Screen() # 画面を作ります。Screenクラスのインスタンスを作っています。
scr.title('draw a heart') # 画面の上にこのタイトルが表示されます
scr.setup (width, height, 0, 0) # 画面のサイズです
ttl = turtle.Turtle() # Turtle オブジェクト（絵を描くカーソル）を作ります
ttl.speed(3) # 絵を描くスピードを設定します
ttl.shape('turtle') # カーソルは'turtle'(亀)にしました
ttl.screen.screensize(width+100, height+100) # この範囲まで画面をスクロールできます。タートルが画面外に行った時、追いかけられるように大きめに設定

ttl.pencolor('red') # ペンの色を赤に設定
ttl.fillcolor('red') # 塗りつぶしに使う色を赤に設定
ttl.pensize(1) # ペンの太さを1に設定

ttl.begin_fill() # ここから塗りつぶし開始
draw_my_heart(ttl, x, y, r) # ハートを描く。デフォルト値を決めてる引数alpha=45, theta=210, degrees=0は省略されています、
ttl.end_fill() # ここまで塗りつぶす

ttl.hideturtle() # カーソルを見えないようにする
scr.exitonclick() # 画面をクリックしたら終了する

ハート曲線を利用して描いたハート

x,y座標をパラメータtで表す

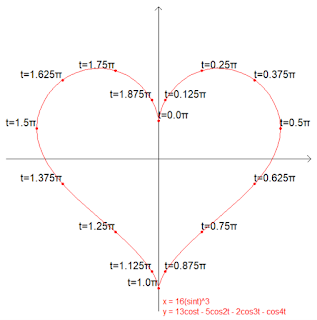
\begin{eqnarray*} x & = & 16 \sin^3 t\\ y & = & 13 \cos t -5 \cos 2t - 2 \cos 3t - \cos 4t \end{eqnarray*}

ハート曲線（heart curve) と呼ばれる曲線はたくさん存在します。 今回、パラメータt (0～2π)によってx,y座標を表し、ハート曲線のグラフを描いてみました。

ちなみに上の図は 説明用に描いたハート曲線（turtleモジュールを使用）です。 ハートの中心より少し上からスタート(t=0)。 時計回りに一周して一番最初の場所に戻ってきます(t=2π) 。

ハート曲線を描くプログラム(matplotlib使用)のソースコード

まず、2つのライブラリmatplotlib, numpy をインストールしておく必要があります。 コマンドプロンプトを起動して下のコマンドを入力すれば、2つのライブラリはインストールされます。 

pip install matplotlib numpy

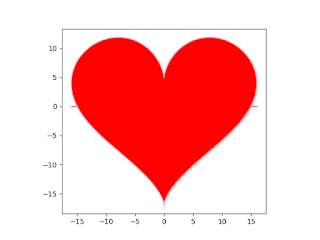
これがmatplotlibとnumpyを使ってハート曲線を描くプログラムのソースコードです。 「図のインスタンスfig」 や 「座標軸のインスタンスax」 を作って、オブジェクト指向的にグラフを描きました。 

# matplotlib.pyplotモジュール をインポートし、pltと略して使います。plt.show()のように使用できます
import matplotlib.pyplot as plt

# numpyライブラリ をインポートして、npと略して使います。np.arange()のように使用できます。
import numpy as np

# グラフ上の点を作成します。それらの点が線でつながれると、ハート曲線のようなグラフができます

# t: 0から2πまで0.01間隔で並んだ数字の配列(ndarray)。パラメータt。
# right_t: ハート曲線の右端の点に来る時のtの値=π/2
# right_y: ハート曲線の右端の点に来る時のy座標の値
# x: グラフ上の点のx座標の配列(ndarray) をパラメータtを用いて表します
# y: グラフ上の点のy座標の配列(ndarray) をパラメータtを用いて表します。

t = np.arange(0, 2*np.pi, 0.01) # np.pi は円周率
right_t = np.pi/2
right_y = 13*np.cos(right_t)-5*np.cos(2*right_t)-2*np.cos(3*right_t)-np.cos(4*right_t)
x = 16 * np.sin(t) ** 3
y = 13 * np.cos(t) - 5 * np.cos(2*t) - 2 * np.cos(3*t) - np.cos(4*t)

# ここから図を作ります

fig = plt.figure() # Figure(図)のインスタンスfig。何も描かれてない図。
ax = fig.add_subplot(1,1,1)  # 座標軸(axes)のインスタンスax を作ります。グラフを描く前に座標軸を決めます。
ax.set_xlim(-17, 17) # x軸を表示する範囲を -17から17 とします
ax.set_ylim(-20, 13) # y軸を表示する範囲を -20から13 とします
ax.plot(x, y, color='pink') # 点(x,y)を順番にピンクの線でつなぎます
ax.fill_between(x, y, y2=right_y, color='red') # 点(x,y) で囲まれた領域を赤く塗りつぶす
ax.set_aspect(1) # x,yの目盛りの比を1にします

# グラフを表示
plt.show()

matplotlib.pyplot を使用し、オブジェクト指向的にグラフを描きました

下の２つのモジュール（ライブラリ）を使ってハート曲線を描きました。

  • matplotlib.pyplotモジュール（グラフを描くのに利用）
  • numpyライブラリ（グラフの線を通す点の集まりを作るのに利用）

これがハート曲線（内部は赤く塗りつぶされている）を描いた手順です。

  1. グラフの線を通す点を作成する（np.arrange()を使用）
  2. 図のインスタンスfig を作成(fig = plt.figure())
  3. 座標軸(axes)クラスのインスタンスax を作成（ax = fig.add_subplot(1,1,1)）
  4. グラフ上の点(x,y)を順につないでハート曲線を描く(ax.plot(x, y, color="pink") )
  5. ハート曲線の内部を赤く塗りつぶす(ax.fill_between(x, y, color="red")）

境界線と内部の色が同じでいいなら、赤く塗りつぶす作業だけすれば良いです。 点が多い方が綺麗に仕上がります。グラフの精度は点の多さに依存します。

縦横の目盛りの比が自動で調整されることがあるので、 ax.set_aspect(1) のようにして、縦:横 = 1:1 にしておいたほうがいいです。

set_aspect()は Axesクラス (座標軸のクラス)のインスタンスax が持っているメソッド（関数みたいな物） です。plot(), fill_between() もAxesクラスのメソッドです。 詳細は matplotlibのAxesクラスのドキュメントに記載されています。

最初、座標軸クラスのインスタンス が グラフを描けることに驚きましたが、 axes は axis（軸）の複数形 なので、 「ある平面の座標軸(x,y軸)」のクラスみたいな感じに思っておけば良いかもしれません。 1つ1つの軸ではなくて。

fill_between() のドキュメント によると、2番目の曲線y2 が デフォルトで y2=0 と設定されてるようです。 そのせいで、y=0 の線が塗りつぶされていました。

そこで、ハート曲線のx座標が最大となる時のy座標を求めて、それをy2としました。 すると、綺麗に赤い線が消えました。

ハートを100個描いてみました(matplotlib使用)

add_subplot() を利用して、図を10x10分割して、100個のハートを描いてみました。

ハートを100個描くプログラムのソースコード

100個のハートを描くプログラムのソースコードはこちらです。 

# matplotlib.pyplotモジュール をインポートし、pltと略して使います。plt.show()のように使用できます
import matplotlib.pyplot as plt

# numpyライブラリ をインポートして、npと略して使います。np.arange()のように使用できます。
import numpy as np

# グラフ上の点を作成します。それらの点が線でつながれると、ハート曲線のようなグラフができます

# t: 0から2πまで0.01間隔で並んだ数字の配列(ndarray)。パラメータt。
# right_t: ハート曲線の右端の点に来る時のtの値=π/2
# right_y: ハート曲線の右端の点に来る時のy座標の値
# x: グラフ上の点のx座標の配列(ndarray) をパラメータtを用いて表します
# y: グラフ上の点のy座標の配列(ndarray) をパラメータtを用いて表します。

t = np.arange(0, 2*np.pi, 0.01) # np.pi は円周率
right_t = np.pi/2
right_y = 13*np.cos(right_t)-5*np.cos(2*right_t)-2*np.cos(3*right_t)-np.cos(4*right_t)
x = 16 * np.sin(t) ** 3
y = 13 * np.cos(t) - 5 * np.cos(2*t) - 2 * np.cos(3*t) - np.cos(4*t)


# 図を10x10分割してハート曲線のグラフを100個描きます

fig = plt.figure() # Figure（図）のインスタンスを作ります。今これは何も描かれていない図。
ax = [] # 座標軸のリスト。空のリストに初期化。
n=10
for i in range(n*n): # i=0,1,2...,n*n-1(=99)に対して以下の操作を繰り返す
    ax.append(fig.add_subplot(n, n,i+1)) # 図をnxnに分割して、左上から数えてi+1番目の座標軸をaxに追加
    ax[i].set_xlim(-17, 17) # 表示するx軸の範囲を-17から17に設定
    ax[i].set_ylim(-20, 13) # 表示するy軸の範囲を-23から10に設定
    ax[i].set_aspect(1) # x軸とy軸の目盛りの比を1に設定
    ax[i].set_axis_off() # 座標の軸、目盛り、枠などを表示しないようにする
    ax[i].fill_between(x, y, y2=right_y, color='red') # 点(x,y)で囲まれた領域を赤く塗りつぶします
plt.show() # グラフを表示

回転させたハートを描く

turtleモジュールを使って、回転させたハートを描くとしたら、最初に向いてる角度を調整します。 下の絵はturtleモジュールによって描かれました。

matplotlib.pyplotモジュールを使って、回転させたハートを描くのに、 いわゆる回転行列(rotation matrix)を使いました。下の絵はmatplotlib.pyplotを使って描かれました。

下の絵は360°/5＝72°ずつ回転させたハート曲線です。

真ん中ある五角形ぽい図形が思ったより綺麗でびっくりしました。

ラベル: , , ,

0 件のコメント:

コメントを投稿

投稿されたコメントは承認後に公開されます。

登録: コメントの投稿 (Atom)